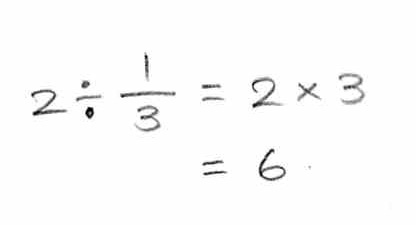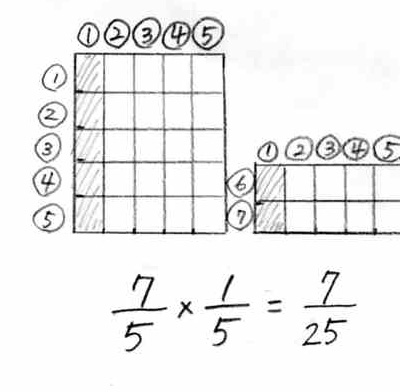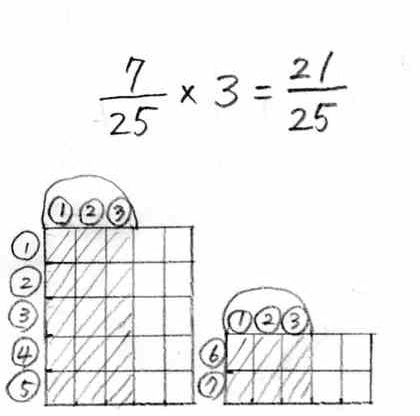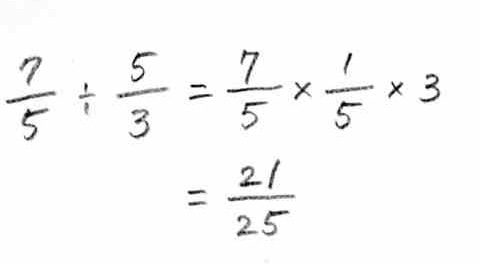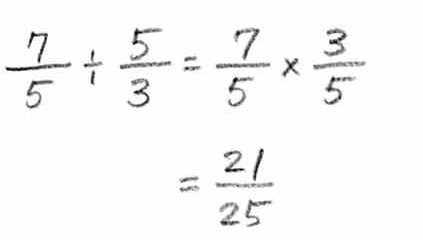�y�������z
http://plaza.rakuten.co.jp/clematis1010/diary/200901130000/
2009.01.13 �����̂��Z�^����Z�̖{���̈Ӗ� �u���w���̕�(13302)�v [ �ǂ��y��
]����
�������A�C���[�W�t�B�b�N�X�@���g���āA���[���������o���錻��ɗ������������������ł����A
���͂�����������������Ƃ�����܂����B�����̂��Z�ł��B�����A�ǂ��y���ɏo��������A
�Z���̕����ň�Ԋ��������̂��A�w����Z�̖{���̈Ӗ��x�Ƃ����Ƃ���ł����B
������Z���āu�������������Ƃ��̂P�����܂�̐��H�v
�����Ⴀ�u3/2(2����3)��1/5(5����1)�v�͂ǂ��Ȃ�́H
���[���ł��Ȃ��������A�[���ł��Ȃ��܂܂�
�u�����̊��Z�͊��鐔�̋t�����|��������v�Ƌ�����āA
���Z�̈Ӗ����m�炸�Ɍv�Z�����͂ł���悤�ɂȂ��Ă��܂��B
����ł͉��p�͈͂炿�܂���B
�����A���w�Z�̎��ɋ������Ĉȗ��A�����Ŋ��鎞�́A�Ђ�����Ԃ��Ă�����A�Ɗۊo�����Ă�����ł����A�[���������������������A�Ƃ����Ǝv���Ă��܂����B
���L��(��)�̈Ӗ�
�@A��B��A�FB��A/B���܂�A�u�a����ɂ����Ƃ��ɑΉ�����l��A�Ƃ���v�@�Ƃ����L���ł��B
���u����Z������v�Ƃ́A�uA����B�v=��A��B���ɂ����āA�(B)���P�ɂ����Ƃ�(�u����������)�ɑΉ�����A�����߂�A
�Ƃ������Ƃł��B
���̐����ɂ́A�ق�܂Ɋ������܂����BA��B�����鎞�́A��iB�j���P�ɂ��悤�Ƃ����炢����ł��B�܂�́A����Z�Łu�P�l�̎�蕪�v���l����A�Ƃ������Ƃł��B���̍l��������{�ɂ���AB�������ł����Ă������ł����Ă��������Ƃł��BB�������Ȃ�AA��B
= A/B�@�ƒP���ɏ����Ă��������A�������Ă��������A�K�v�Ȃ�M�Z�œK���ȂƂ���܂Ōv�Z���Ă������BB�������Ȃ�A������P�ɂ��邽�߂ɁA���ǂ̂Ƃ���́u�Ђ�����Ԃ��Ă�������v�����BB�������Ȃ�A�i0.4�Ȃ�@�S�^�P�O�Ƃ����悤�Ɂj������ɒ����āA�����悤�ɂ������B�E�E�E�E����������������I�I�i�ƁA����Ƃ��͌���ւ������ǁj�ۊo�����Ȃ���[�Ȃ��A�Ƃ�����߂Ă������Ƃ̐������A�v�������������āA�킽���A�ǂ�搶�ɂ��čs�����A�ƌ��S�����u�ԁi�j�ł����B�����̂��Z���w�Z�ŏK���̂́A���U�ł��B���[�ɂ����U�܂ł�点�����͂���܂���ł����B�ł��A�����A���Ƃ̕��ɐ������Ă������̂Ƃ��̗���ŁA�i�܂������f�̏�Ԃ̎q�ǂ����A������������ǂ��l���邩�ȁH�j�Ƃ�����������`���āA�����Ă݂܂����B�u��肽���Ȃ�������A����ł������˂ǁE�E�E�P���P�^�R�@�A����Ă݂�H�v�����ŁA���̈Ӗ����ӂ����ѐ������܂����B�u�����Ă����̂́A����Z�ŁA�P�l���͂����ɂȂ�܂����A���Ă������Ƃ�������Ȃ��B�����R�A�������A�R�l���Ł��Ȏ��A�P�l���͂ǂ��H���Ă������Ƃ��H�P�^�R�l���Ă����̂́A�l������R���C���ǁA�G��`���čl���Ă݂Ă���ւ�H�v���[�́A���炭�l���Ă���A�u����Ȃ����낵���l��`���́`�H�ӂ��ӂ��Ӂ`�v�@�ƁA�������ꂵ�����ɕ`���͂��߂܂����B�u���`�`�`�H�H�@�R�Ԃ�̂P�l�A�R�Ԃ�̂P�l�E�E�E�����傭�����C�Ȃ��B�����i���j�̕����łP���Ă��Ƃ��Ȃ��H������Ƒ҂��Ă�`�`�ق�Ȃ�A�P�l�������`�`�`�R�I�I�@�E�E�E�����Ă�H�H�v�u�吳���I�I�v�����ŁA�F�C���o���āA����������ƕ����Ă݂܂����B�u�ق�Ȃ�ȁ`�A����͂ق�܂ɓ���`�`�`��l�ł����͓���`�`�`����A�ł���ł����˂ǁA�P���S�^�R�@�A���čl���Ă݂Ă���ւ�H�@�G��`���āB�v���[�́A�܂����Ă��A�����낵���G��`���n�߂܂����B�i���̎��`�����G�͎��Ƃɒu���ė��Ă��܂����̂ŁA���ɖ߂��ė��āA���Ƃ�����ɐ������鎞�ɕ`�����G���ڂ��܂��B���܂��ܒ���u����ڎ��̗����g�����̂ŁA�搶�̎ʐ^��������Ɠ����Ă܂��B�j
���ꂪ�S�^�R�l���H�ق�ŁA�L�����f�B�[���P�Ȃ���Ȃ��B���̐l�́A�R�Ɋ���ĂāA�i�|���j���ꂪ�S�Ԃ���Ă��Ƃ��H�@�i�|���j���̂S�Ԃ�ŃL�����f�B�[�P�B���₩��A�L�����f�B�[�P���S�ɕ�����˂�B���̐l�́A���̂R�Ԃ�łP�l�̐l�Ԃ₩��A�P�l���Ă����̂́A�R�Ԃ�A�L�����f�B�[���R�Ԃ�₩��E�E�E�L�����f�B�[3/�S�I�I�@�@�����Ă�H�H�ǂЂႠ�`�`�吳���ł������܂��I����ς�A�G�̗͂��Ă������I�I�@�Ȃ��Ȃ����イ���̂������ł������܂����B
Last updated� 2009.01.13 07:25:53
�http://plaza.rakuten.co.jp/clematis1010/diary/200902220000/
2009.02.22 ���Z�́A����Z�� �u���w���̕�(13301)�v [ �ǂ��y�� ]����
�����̂��Z�ɂ����̋L���ւ̕⑫�ł��B����Z�̖{���̈Ӗ���ǂ�Ŋ��������R�N�O�A�Q�O�����炢������Ď���̑��̃}�}�B�ɔz�������ǁA�N�ЂƂ�A�킩�����ƌ����Ă��ꂽ�l�͂��܂���ł����B�Ȃ�Ƃ������ʖ�ł��Ȃ����A�ƁA�������O����l���Ă��āA�ǂ�搶�ɂ����₳���Ă��������āA�Ȃ�ƂȂ������܂Ƃ܂��Ă��܂����B
������Z�F�u����Z������v�Ƃ́A�uA����B�v����A��B���ɂ����āA��iB�j���P�ɂ������i�u�����������j�ɁA�Ή�����A�����߂�Ƃ������Ƃł��B
�E�E�E������Ɠ���ł���ˁB���Z�͂���Z����{�ɂ��čl����ƁA�킩��₷����ł��B
�C�����I����Ƃ��A������Q�b�g���܂����B���̂�����A���ɂȂ�Ȃ��悤�ɁA
�݂�ȓ��������炦��悤�Ɂi�ϓ��Ɂj�����܂��B���̎��A�u�P�l�̕����O�����ɂȂ邩�v�����߂�̂��A����Z�ł��B
���L���i���j�̈Ӗ�
�@A��B��A : B��A/B
�@���܂�uB����ɂ����Ƃ��ɑΉ�����l��A�Ƃ���v�Ƃ����L���ł��B
A��B�AA : B�AA/B�́A�\�����Ⴄ�����ŁA�������Ƃ�\���Ă���̂ł��B
�ǂ�搶�ɂ��ƁA���̕\���̈Ⴂ�́A�u���{��A�C�^���A��A�t�����X��݂����Ȃ��́v�������ŁA�ǂ�����ǂ̂Ƃ���́AB�ɑ���A
�Ƃ������ƂȂ�ł��B����Z�I�ɕ\������ƁA�C����B�l��A�̂�����Q�b�g�B���Ⴀ�A�P�l���́H�Ƃ������ƂɂȂ�܂��B
����́A����Z�̊�{�̍l�����ŁA���̂��Ƃ����킩��A���鐔�ɉ������Ă��ւ������ł��B�u�P�l�̎�蕪�v�����l���������ł�����BA��B�ɋ�̓I�Ȑ��������āA�l���Ă����܂��傤�B
���U���R��6 : 3�@�i�R�ɑ��ĂU�j
�����ŊC�����I�������Ƃ��o��ł��B
�`�C�����I�������Ƃ��A������Ԃ�ǂ��Ă��܂����B�`
�C���R�l�ŁA����U���Q�b�g�I������G�ŕ`���ƁA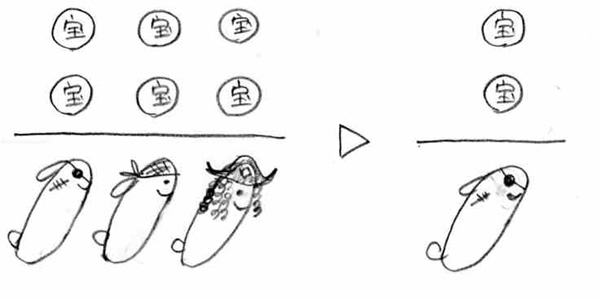 �P�l���͂Q�B�G�ɕ`���ƈ�ڗđR�ł��ˁI�����ŏ����ƁA
�P�l���͂Q�B�G�ɕ`���ƈ�ڗđR�ł��ˁI�����ŏ����ƁA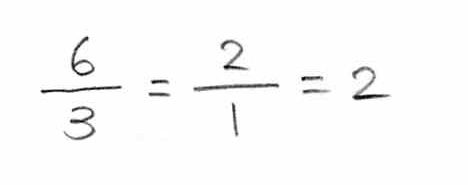 �ƂȂ�܂����A����́A
�ƂȂ�܂����A����́A
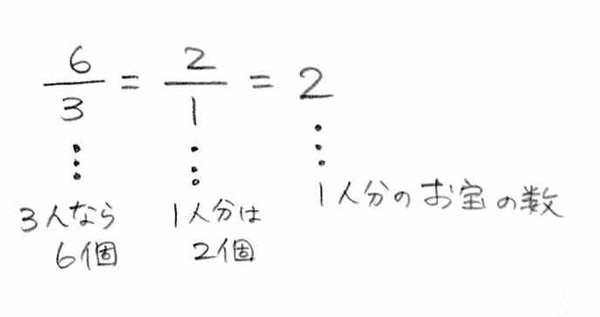
�Ƃ������ƂŁA����͂ǂ���������A�܂�A�u�P�l�Ԃ�̂���̐��v��\���Ă��܂��B�O�p���Z�\�ł́A
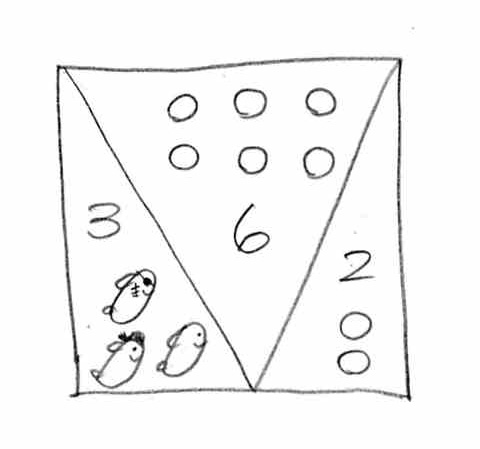
�ƂȂ�܂��B
���Q���@�P�^�R�@���Q�F�@�P�^�R�@�i�P�^�R�ɑ��ĂQ�j
�C���P�^�R�l�Łi�N���ɐ�ꂿ�������ł��傤���H�H�j����Q�Q�b�g�I�P�^�R�l�i�P�����j�ł���Q�ł��B

�̂��P�l���ɂ��邽�߂ɂ͂R�{��������̂ŁA
������R�{���āA�U�B
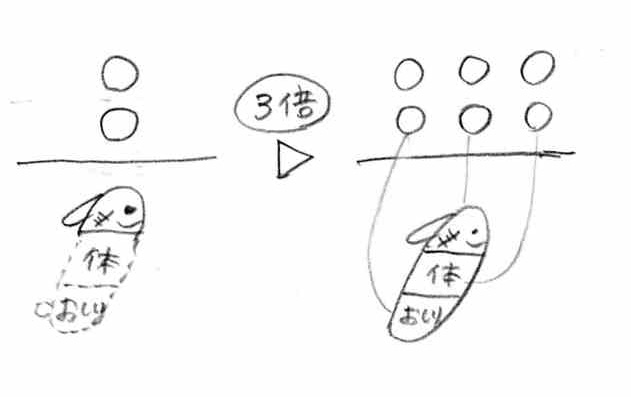
���ŏ����ƁA
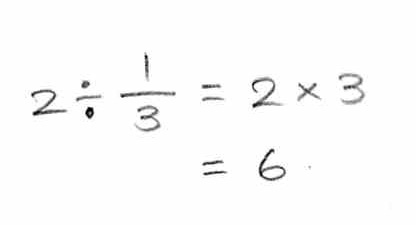
�ƂȂ�܂��B
���Q���@�S�^�R�@���Q�F�@�S�^�R
�C���S�^�R�l�ŁA����Q�Q�b�g�I
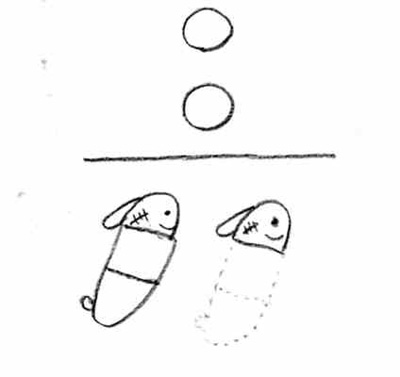
���̊G���悭����ƁA�C���̑̂͂S��������Ă��܂��B������A������S�������܂��B
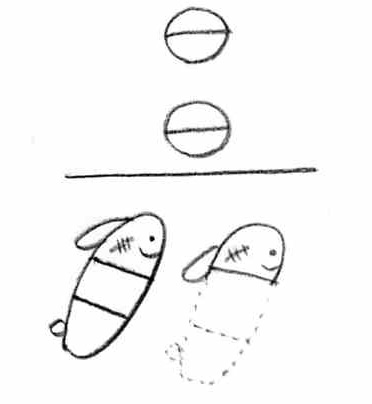
��ꂽ�̂̂R���������킹��ƂP�l���̑̂ɕ�������̂ŁA������S�����������́i�P�^�Q�j�̂R�Ԃ�A�܂�R�^�Q���P�l���̕����O�ƂȂ�܂��B
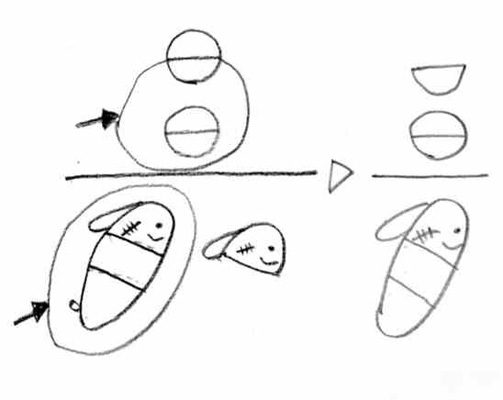
������S�������āE�E�E�R�Ԃ�A�Ƃ����Ƃ�������ɕ\���ƁA
�S�������āE�E�E�^�S
�R�Ԃ�E�E�E�~�R
�~�R�^�S
�ł��B
���q�i�S�j�Ŋ��������̂��i���q�Ŋ����āj�A����i�R�j�Ԃ�p�ӂ���i�����������j�A�P�l�Ԃ�̑̂��ł�������܂��B���́A���q�Ŋ����āA�����������A�Ƃ����Q�X�e�b�v���A�P�̎��ŕ\���ƁA
X�@����^���q
�ƂȂ�܂��B�u�����Ŋ��鎞�́A���q�ƕ�����Ђ�����Ԃ��āA������B�v
�Ƃ������Ƃ̈Ӗ��́A�����������Ƃł��B
�����鐔�������̏ꍇ���l���Ă݂܂��傤�B
���V�^�T�@���@�T�^�R�@���@�V�^�T�F�T�^�R�@�i�T�^�R�ɑ��ĂV�^�T�j
�C���V�^�T�l�ŁA���T�^�R�Q�b�g�I
����̂���͎l�p�`�ɂ��܂��ˁB
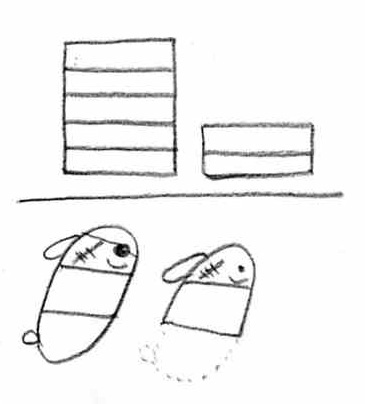
���̐}�ł��C���̑̂͂T�̕����ɕ�����Ă��܂��B������P�l���̑̂ɂ���ɂ́A�T�Ŋ����āE�E�E�i�^�T�j
���̂R�Ԃ�iX�R�j

�܂�AX�@�R�^�T������ƁA���I������P�l���ɕ������܂����B���������ɍ��킹�āA�c�ɂT�Ɋ����āA
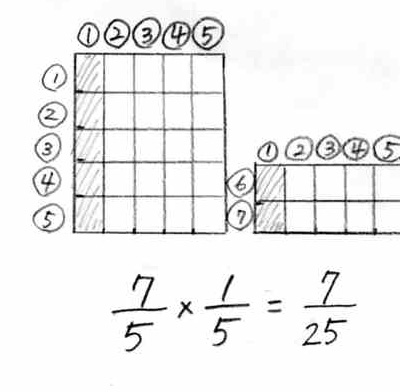
���̂R�Ԃ�A
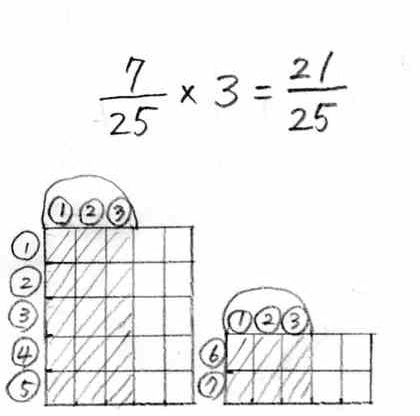
�܂�A�Q�P�^�Q�T�������ł��B���̌o�߂����ŏ����ƁA
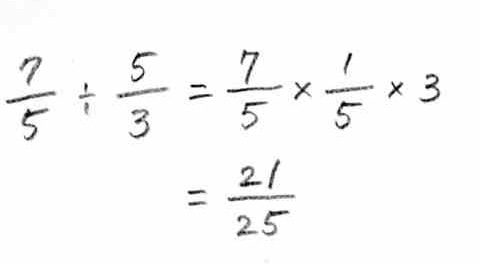
�ȗ������Ď��ɏ����ƁA
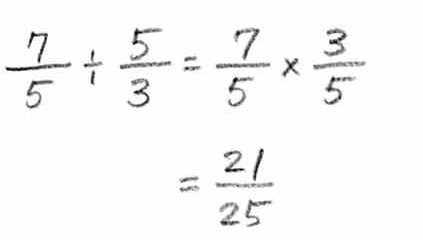
�ƂȂ�܂��B����ŁA�����ǂ��Ȃ��Ă�����Z�͑��v�ł��ˁI�����A����Ƃł����B�O�̋L���ƍ��킹�ăR�g�m�n�̌��e�ɂ��܁`���B
Last updated� 2009.02.22 10:48:11

 �P�l���͂Q�B�G�ɕ`���ƈ�ڗđR�ł��ˁI�����ŏ����ƁA
�P�l���͂Q�B�G�ɕ`���ƈ�ڗđR�ł��ˁI�����ŏ����ƁA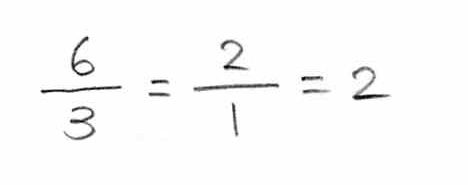 �ƂȂ�܂����A����́A
�ƂȂ�܂����A����́A