分数は数字ではありません。割合を表している記号です。
それを、整数や小数と同じ感覚で説明していては分からない方が普通です。
4/2(2分の4)とは4÷2を表しているだけで、一般的な数字を表してなどいないのです。
2を基準としたときに4に当たる(相当する)数を表している記号です。
だから基準を変えても同じ割合のおおきさを分子におけば=になるのです。
つまり4/2=2/1=2=6/3........。ですから、分数とは数字ではないということです。
実は数は全て1が基準になっているのです。
ところが分数は分母が基準になっています。
ということは普通の数字と同じように教えてはいけないし、同じような考え方では理解できないのが当然なのです。
もちろん1を基準にした分数は整数と同じになります。1分の3(3/1)=3。なぜなら、普通の数字は基準が1だからです。
こんな基本も知らずに分数を教えている先生がいる。しかも大勢いる。これでは子供に負担ばかりがかかってしまう。
……………………………………………………………………………………………
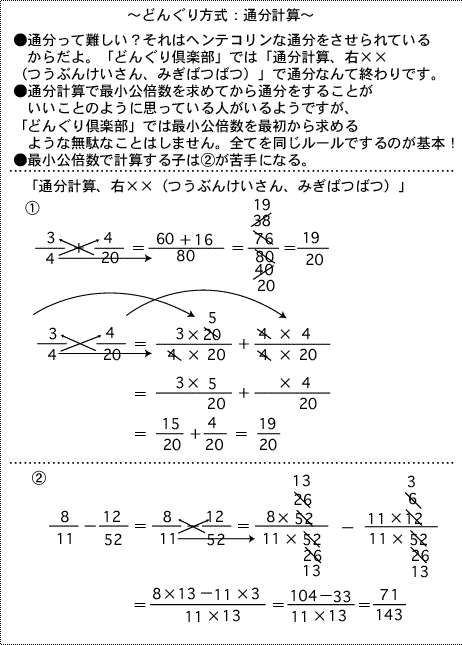
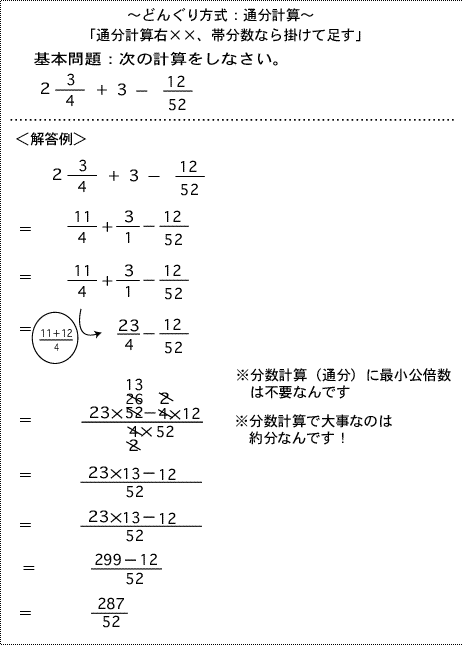
●分数の加減で最小公倍数を使う必要がない理由
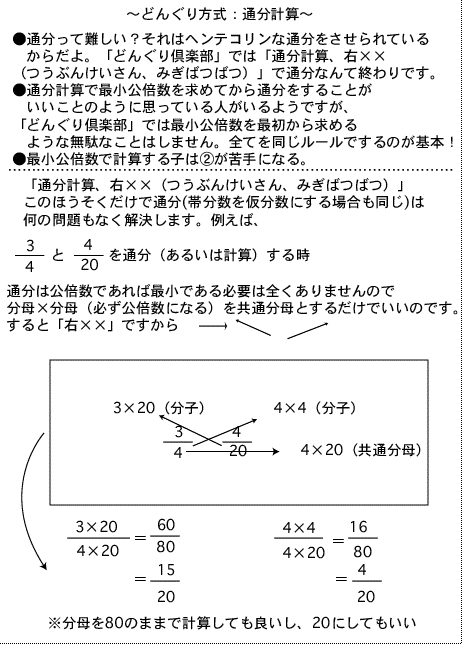
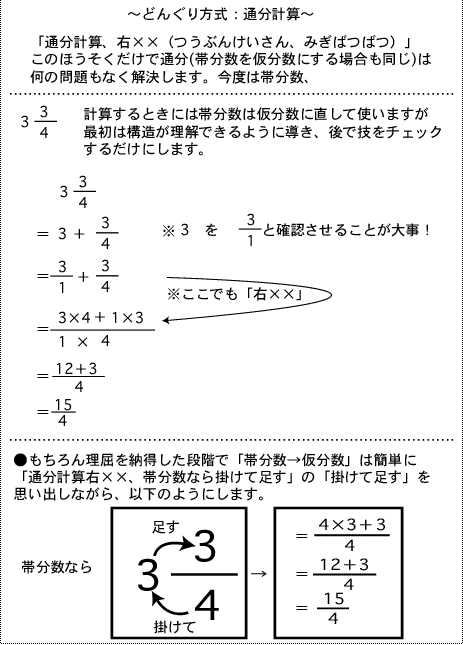
分数の足し算・引き算では基準を統一するために、通分(分母を揃えること)をしますが、この時に「最小公倍数で通分します」
と教える先生がいますが、これは基本ではありません。
通分とは、基準を揃える(同じ土俵にのせる)ということだけですから共通な倍数(公倍数)であれば何でもいいのです。
つまり、分母×分母を共通分母にするだけで100%できるのです。最小公倍数で頭を悩ますことは不要なのです。
先日、中3に三平方の定理を使って直角三角形の1辺の長さを計算させていたら
「計算できません」という
よく見ると、分数の計算ができないらしい。
「通分できません」という
よく話を聞くと、通分は最小公倍数でするものだと思い込んでいて、その最小公倍数が出せないから計算できないということらしい。
つまり、正しい基本計算を教わっていないのです。
<計算>分数の2乗を展開して下記のようになったところで、基本を教えてもらっていない子は計算停止
100/49 + 75/16
=????
ところが、基本を知っている子は、何の抵抗もなく続けます
100×16/49×16 + 75×49/16×49
=(1600+3675)/49×16
=・・・・・・
※小学校で、常に最小公倍数探しをしていた子は、最小公倍数が直ぐに見つかる分数の計算しかできません。
貴重な時間を使って、計算さえもできない応用の利かない頭を育てていると言うことです。
■さらに悪いことには最小公倍数を使った基本的な下記のような問題さえもできなくなる子が多くなるようです。
………………………………………………………………………………………………
<5MX86>
4と7の最小公倍数を分母、最大公約数を分子にした分数と、
4と12の最小公倍数を分母、最大公約数を分子にした分数とを足すと
幾(いく)つになりますか。
………………………………………………………………………………………………
答え:31/84(84分の31)
●「どんぐり方式」分数計算(通分・帯分数・基本計算1.2)
●本当の基本を知っていると「開成中学」でもへっちゃらなんです!→実際の入試問題

