|
������Z(���ɕ����ł̊��Z)�̋������ɂ��Ă̎��₪�����̂Ő������܂��B
�����w���ɂ́u�`�ɂ��v�u�`�ɑ��āv�u�`������v�u�`�ɑΉ�����v�Ȃǂ͓�����t�ł������x���������Č��t�̗����������邱�ƁB
������Z���āu�������������Ƃ��̂P�����܂�̐��H�v
�����Ⴀ�u3/2(2����3)��1/5(5����1)�v�͂ǂ��Ȃ�́H
���[���ł��Ȃ��������A�[���ł��Ȃ��܂܂Ɂu�����̊��Z�͊��鐔�̋t�����|��������v
�@�Ƌ�����Ċ��Z�̈Ӗ����m�炸�Ɍv�Z�����͂ł���悤�ɂȂ��Ă��܂��B
�@����ł͉��p�͈͂炿�܂���B
�����������Z�̋�����
������Z��������Ƃ��ɂ͎g���Ă���L���̈Ӗ��������Ȃ���i�݂܂��B
���L��(��)�̈Ӗ�
�@A��B��A�FB��A/B���܂�u�a����ɂ����Ƃ��ɑΉ�����l��A�Ƃ���v�Ƃ����L���ł��B
������Z
�u����Z������v�Ƃ́uA����B�v=��A��B���ɂ����Ċ(B)���P�ɂ����Ƃ�(�u����������)��
�@�Ή�����A�����߂�Ƃ������Ƃł��B
��10��2��10�F2��(������P���~1/2)��10�~1/2�F2�~1/2��5�F1������5
����2�ɑ���10���Ȃ��1�ɑ��Ċ�H�����2��1�ɂ���ɂ́~1/2
�� 2��6��2�F6��(������P���~1/6)��2�~1/6�F6�~1/6��1/3�F1������1/3
����6�ɑ���2���Ȃ��1�ɑ��Ċ�H�����6��1�ɂ���ɂ́~1/6
��1/2��2/5��1/2�F2/5 ��(������P���~5/2)��1/2�~5/2�F2/5�~5/2
��5/4�F1������ 5/4
����2/5�ɑ���1/2���Ȃ��1�ɑ��Ċ�H�����2/5��1�ɂ���ɂ́~5/2
��7/3��6/11��7/3�F6/11��(������P���~11/6)��7/3�~11/6�F6/11�~11/6��77/18�F1������77/18
����6/11�ɑ���7/3���Ȃ��1�ɑ��Ċ�H�����6/11��1�ɂ���ɂ́~11/6
���ȏ�̂悤�ɋ�����ƑS�Ė������ƂȂ��v�Z�ł���悤�ɂȂ�܂��B
���ߑ��u�~�Ɓ��͔��̈Ӗ���\���Ă��鐔�w��ł��v
��A�~B���P�ɑ���l��A�̂Ƃ��AB�ɑ���l��\���Ă���
��A��B�� B�ɑ���l��A�̂Ƃ��A�P�ɑ���l��\���Ă���
�@�@�@�@�@���~�̑O�̃R���͒P�ʗʄ
���|�Z�������~A���P�ʗ�(�P�ɑ����)�����g���āAA�ɑ���ʂ����߂�Ƃ�������
�@��
�t�̈Ӗ�
�@��
�����Z��������A��A�ɑ���ʁ����g���āA�P�ʗ�(�P)�ɑ���ʂ����߂�Ƃ�������
�@�@�@�@�@�����̑O�̃R����A�ɑ����
���P�ʗʂ��P�l�ł��炦��ʂƌ����Ǝ��̂悤�ɂȂ�
�@�@�@�@�@�@�@�@�@�@���������O�ɂP�l�ł��炦��ʂ������Ă���̂ŁA�R�l�ł��炦��ʂ����߂Ȃ���
�����������������������@�@���������������������@
���P�l�ł��炦������~�R�����R�l�ł��炦��ʄ�
���������������������@�@�@��������������������
��F�P�T�~�R���S�T(�P�l�ł��炦��ʂ��P�T�Ȃ̂ŁA�R�l�ł��炦��ʂ͂P�T�~�R���S�T)
�@�@�@�@�@�@�@�@�@�@���������O�ɂR�l�ł��炦��ʂ������Ă���̂ŁA�P�l�ł��炦��ʂ����߂Ȃ���
�����������������������@�@���������������������@
���R�l�ł��炦��������R�����P�l�ł��炦��ʄ�
���������������������@�@�@��������������������
��F�P�T���R���T(�R�l�ł��炦��ʂ��P�T�Ȃ̂ŁA�P�l�ł��炦��ʂ͂P�T�^�R���T)
�@�@�@�@�@�@�@�@�@�@�@�@���������O��1/3�l�ł��炦��ʂ������Ă���̂ŁA�P�l�ł��炦��ʂ����߂Ȃ���
���������������������������@�@�@�@���������������������@
���P�^�R�l�ł��炦��������P�^�R�����P�l�ł��炦��ʄ�
�������������������������@�@�@�@�@��������������������
��F�P�T���P�^�R���P�T�~�R���S�T(�P�^�R�l�ł��炦��ʂ��P�T�Ȃ̂ŁA�P�l�ł��炦��ʂ͂P�T�~�R���S�T)
�@�@�@�@�@�@�@�@�@�@���������O�ɂT�l�ł��炦��ʂ������Ă���̂ŁA�P�l�ł��炦��ʂ����߂Ȃ���
�����������������������@�@���������������������@
���T�l�ł��炦��������T�����P�l�ł��炦��ʄ�
���������������������@�@�@��������������������
��F�Q�^�R���T���Q�^�R�~�P�^�T���Q�^�P�T
�@(�T�l�ł��炦��ʂ��Q�^�R�Ȃ̂ŁA�P�l�ł��炦��ʂ͂Q�^�R�~�P�^�T���Q�^�P�T)
�@�@�@�@�@�@�@�@�@�@�@�@���������O��1/6�l�ł��炦��ʂ������Ă���̂ŁA�P�l�ł��炦��ʂ����߂Ȃ���
���������������������������@�@�@�@���������������������@
���P�^�U�l�ł��炦��������P�^�U�����P�l�ł��炦��ʄ�
�������������������������@�@�@�@�@��������������������
��F�Q�^�R���P�^�U���Q�^�R�~�U���P�Q�^�R���S
�@(�P�^�U�l�ł��炦��ʂ��Q�^�R�Ȃ̂ŁA�P�l�ł��炦��ʂ͂Q�^�R�~�U���P�Q�^�R���S)
������Z�F��{�`��
����C���킹�u����Z�E�ȒP�F���^�J���A�j���Y�E�A���P�}�G�A�A�}���v�ƃ��Y���ǂ������o���܂��B
������ƗႦ��57��6���̏ꍇ
�u���^�J���A�j���Y�E�A���P�}�G�A�A�}���v
�@�@�@57�@���@�@6�@���@�@9�@�@...3
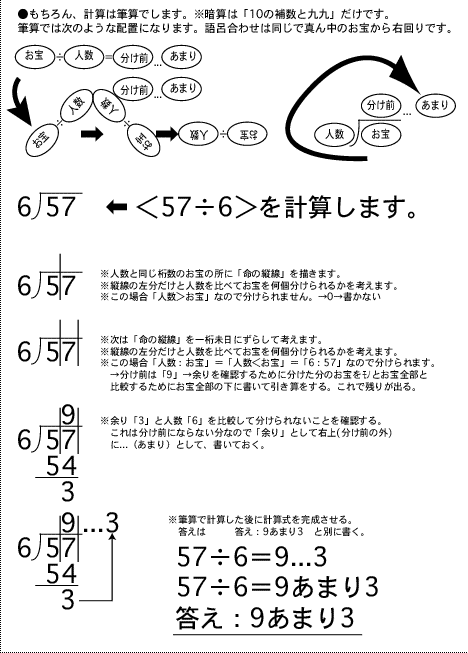
���v�����g�pPDF�t�@�C����DL�i�_�E�����[�h�j�̓R�`����57��6��9...3��
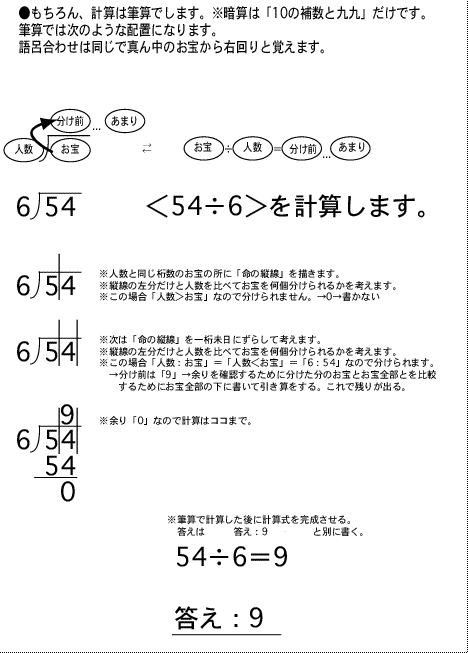
���v�����g�pPDF�t�@�C����DL�i�_�E�����[�h�j�̓R�`����54��6��9��
|


