
※子供自身が作った三角視算表

■三角計算とは何か:視算という計算方法について
子供達に必要な力は「考える力」です。「考える力」とは言葉をイメージ(主に視覚イメージ)化し、
そのイメージを操作する力のことです。今回紹介する「三角計算」は数字の配置をイメージすることで
全ての計算に必要なルールである「10の補数と九九」を最速で導く「視算」をできるようにします。
計算なのに「考える力」の素になる視覚イメージを利用するので、計算力だけではなく考える力の養成にもなります。
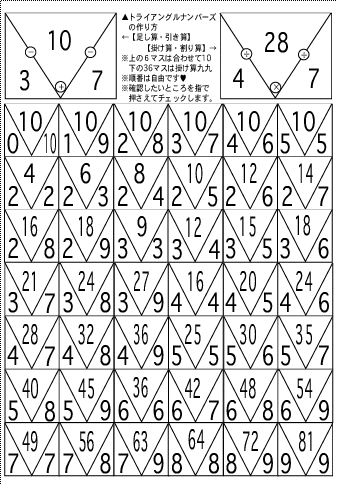
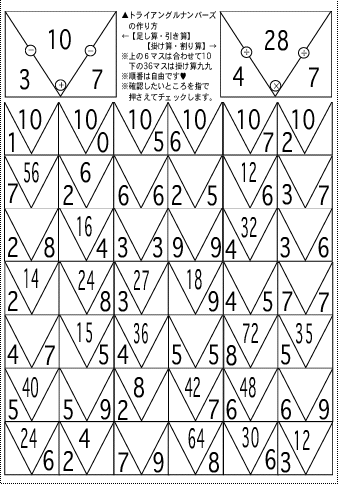
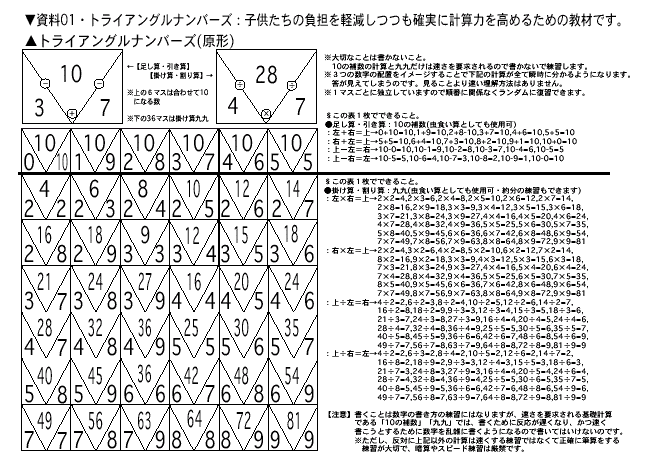
■三角計算でできること■→△の秘密のヒミツ 「三角計算」は暗算の中でも視算と呼ばれるものです。視算は一瞬です。しかも、誰もが簡単にできます。使うのは「10の補数と九九」を△になるように配 置した「三角計算」の表(三角視算表)だけです。「三角計算」は、スピードアップのための練習も不要です。なぜならば、最初から最速だからです。イメージ を再現することより速い人間の反応はないからです。また、視算は頭で使うエネルギーは最小であるにもかかわらず、最大最速の効果が得られますので、究極の 省エネ学習ともいえます。構造は簡単です。<図1>をご覧下さい。最上段が「10の補数」下の六段が「九九」を表しています。つまり、この一枚の表の中に 計算に必要な「10の補数と九九」が全て配置してあるということです。 ハハ図2 <*図1*>:三角視算表(三角計算の全てが記入してある表) では普通の暗算と「三角計算」を比較してみましょう。 1:3×7を頭の中でやってみます。 すると、頭の中では掛け算九九の音声に反応して 3→7→21 と数字が出てきます。 次に、7×3を頭の中でやってみます。 すると、頭の中では掛け算九九の音声に反応して 7→3→21 と数字が出てきます。 次に、21÷3をやってみます。 が、これはできません。割り算の九九 (音声)などないからです。 そこで、3×□=21を頭の中でやり、□=7を探します。 次に、21÷7をやってみます。 が、これもできません。割り算の九九 (音声)などないからです。 そこで、7×□=21を頭の中でやり、□=3を探します。 さて、今度は今やった計算を続けてやって時間を計ります。 ほんの数秒のことだと思いますが、頭の中の様子をよく覚えておいてください。 3×7= 7×3= 21÷3= 21÷7= 2:さて「三角計算」です。「三角計算」では次の構図をイメージするだけです。<図2参照> イメージする時のきっかけとして「九九」の暗唱を「さんしち」まで言えばスッと出てきます。あとはイメージ再現した3つの数字を見るだけで、先ほどの4 つの計算に加えて分数・約分の構造も確認できます。一秒もかからないと思います。この作業は小一でも十分にできます。絵本と同じだからです。「九九」の暗 唱はイメージするときのきっかけとしては大変優れていますので重要項目ですが、苦手ならば三六個で結構です。全段スラスラと言える必要はまったくありませ ん。数字・文字・数式・図形・映像は、音をきっかけとして容易にイメージ化されるからです。ここで大事なのは答えではなく、三角形に配置された3つの数字 のイメージです。この形(映像の配置)が大事なのです。「サン・シチ・ニジュウイチ」と言ったときに3×7=21の21だけを意識する場合と、「三角計 算」で配置までイメージする場合とでは応用力が全く違うということです。3×7=21では、前から3→×→7→=→21と一種類の構造を意識するだけで終 わってしまいます。ところが「三角計算」では3つの数字の配置そのものをイメージするので、3×7=21,7×3=21,21÷3=7,21÷7= 3,21/3=7,21/7=3という6種類の構造を一瞬で意識できるのです。もちろん、分数を教わっていない段階でも配置はイメージできますから、分数 を教わるときに新しく覚え直す必要さえなくなってしまいます。また、3×7=21は数式として見ていますが「三角計算」は絵図としえ見ています。ですから 数式よりも格段に体験的であり、自然に深く理解することができます。さらに、体験は素早く浸透し忘れにくく思い出し易いという性質を持っていますので、基 礎作りには最適です。全ての計算は「10の補数と九九」だけで解けます。ですから、コレだけは視算を使って最高速でできるようにするのです。ただし「九九 が高速でできる」ということと、「三角計算をイメージできる」ということとは全く違うことを忘れないでください。「九九」の練習は「考える力」を育てる三 角計算でするのです。 ■練習 練習は、これら3つの数字の配置を思い出せるようにするだけです。「九九の暗唱」で答えだけを思い出すのではなく、3つの数字の配置を思い出せるように 練習します。<練習法1>三角視算表を見ながら九九を言う:この時に3つの数字の配置をセットで思い描けるように(見える)様にすることが重要です。覚え てしまうと「サンシチ..」で3・7・21の数字の位置が見えるようになりますので、見えた時点で「唱える」ことは止めます。最後まで唱えると反応が遅く なります。<練習方法2>「三角計算」は書き写すという準備段階で、すでに何回も自然に「10の補数と九九」の復習をしていますので、写すだけでも力にな ります。どの△を抜こうか考える度に自然に九九を確認していますし、書く時にもまた、自然に九九を確認しているからです。ですから、少しずつ学習に取り入 れていってください。 ■使い方:「三角計算」3つの使い方 1.九九表として使う:世界で一番コンパクトな九九表です。10の補数表も含んでいる優れものです。 2.四則計算相関表として使う:四則計算(+−×÷)の関係が自然に分かるようになります。 3.視算練習表として使う:最速の基礎計算力(視算)と目で考える力を育てることができます。 ■特徴 1.最速の基礎計算方法「視算」を簡単に修得できます。 2.考える力の素である「イメージ化」の養成ができます。 3.「10の補数」では「分解・合成」の関係が一目で分かります。 4.「九九」では「分数・約分・乗除」の関係が一目で分かります。 5.全ての計算の基礎である「10の補数と九九」の練習が1枚のプリントでできます。 6.見えるようになった時点で誰もが最速ですから、タイムの計測は不要です。 ※三角視算表1枚を意識しながらサッと目を通しただけで<図1>の計算を全て復習したことになります。もちろん分数などを習っていない学年は分数を意識する必要はありませんが、それでも分数の基礎は無意識にできてしまいます。 ■注意 1.「三角計算」の目的は視算のためのイメージ再現です。基礎計算にイメージを利用することで、計算以前の暗記である「10の補数と九九」を単なる暗記から思考力の基本へと引き上げることを可能にするのです。 2.視算が最速だからと言って、すべての計算をイメージ操作でしようとしてはいけません。視算は「三角計算」だけにし、他の計算は全て筆算でします。「10の補数と九九」以外の暗算(筆算以外での高速計算練習)は「考えない習慣」を付けるからです。 ※九九が苦手な人は「三角視算表」をいつも横に置いて筆算を正確にできるようにすれば何の支障もありません。5年生の7月までに(割り算の筆算で確認)できれば十分です。 ■「九九」は全段言えなくてはいけないのでしょうか?:ここで大事なことを確認しておきましょう。「九九」は全段言えなくてはいけないのでしょうか?答え はNOです。「九九」は必ず小さい数から唱えるという約束さえ守れば、三六個でいいのです。「9×3は?」と言われても、頭の中で3×9=27とすればい いのです。どんなに複雑な計算でも、「九九」の大(大きな数)×小(小さな数)を使わなければできない計算などないからです。もちろん、「九九の暗唱」は 重要事項です。それは、音声がイメージを導くからです。しかし、「三角計算」のイメージが浮かべば「九九」は三六個でいいんです。そして、効率的な学習を 考えるのであれば、不要な九九を覚える時間や暗算練習の時間を使って、筆算の構造を理解した方がいいでしょう。「できるからさせる」は「どこで止めるのが もっとも効果的なのか(弊害がないのか)を見極めることができないから、習熟という名の下にさせているだけ」ということになってしまいます。かつて(昭和 初期まで)は「割算九九」も暗記していましたが、今では聞いたこともない人の方が多いでしょう。筆算ができる現代人には不要だからです。まったく同じ事が 多くの時間を割いている今の暗算練習にも当てはまります。※「割り算九九」は「割算書(1622年・毛利重能)」「塵劫記(1627年・吉田光由)」に記 述があります。 ■「10の補数と九九」以外は筆算でする理由:「10の補数と九九」以外は筆算でする理由です。12×2=24くらいは暗算でやれたほうがいいと言う人が いますが大間違いです。複雑な計算をしてみると理由が分かります。912×872=795264の計算に12×2はありますが12×2=24は使わないの です。いいえ、使えないのです。基本計算ではないからそして、基本計算以外の計算は暗算すべきではないし暗算できても何の意味もないのです。こんなことの 練習に時間を使ってはいけないのです。確認します。 912 × 872 1824 6384 7296 795264 どうですか?「10の補数と九九」以外に何か使いましたか?使わないのです。ですから「10の補数と九九」以外の暗算は練習しないのです。筆算ならば誰も が無理なくできること<例えば、2009+37=2046, 68-19=49, 12×4=48, 63÷2=31...1 >などを暗算でする必要は全くありません。なぜなら「穴埋め計算プリント」などを使ってどんなに多くの計算をしても、内容は実は「10の補数と九九」の反 復をしているだけだからです。計算力とは簡単な暗算を高速にできることではありません。視算で「10の補数と九九」を利用しながら億劫がらずに筆算をキチ ンと書く習慣なのです。たとえ一桁の計算でも筆算ですることが大事なのです。暗算でできるようになってもです。筆算を億劫がらずに書くことが計算の基本だ からです。特に、小学生は無駄な計算練習(特に単純計算を暗算ですること)をしている時間はありません。一日も早く良質の文章問題に取り組んで考える力を 育てる必要があるからです。文章問題は指導方法を知らない人が指導すると「考えなさい」というばかりで時間の浪費を招きます。ところが、ここで視考力を使 うと文章問題を楽しく解けて、同時に考える力を育てることができるのです。 ■計算が速くてはいけない理由:速くていいのは「10の補数」と「九九」だけです。他の計算まで速くしては いけません。なぜなら、考える力を養成すべき時期には速さが一番の大敵となるからです。単純作業を速くするには何も考えないで作業に没頭する必要がありま す。また、速い作業をしている時に何かを考えようとしても考えられません。つまり、速い作業は考えることを妨害する作用があるということです。速い作業 (高速計算)をし ている時には頭の中では「考えるな」という指令が出ているということです。集中できているという人がいますが「考えない集中力」をどんなに付けても思考力 は育ちません。計算は速い方がいいという人がいますが、高速計算(視算ではなく計算)の練習に使う時間が「考えない訓練の時間となること」が大きな問題な のです。高速計算をさせて自信や達成感を持たせてはいけないのです。「せめて単純な計算ができるように」という声も耳にしますが、不要な単純計算練習のた めに使っていたエネルギーの一部を視考力の養成に回すだけで「考える力」も同時に育てることができるのです。 ■私の大失敗:私は一時期、5〜400マス計算をさせていたことがあります。計算は速くなるしゲームのようにできるので大人気でした。自信や達成感も持た せられるのでいい方法だと思っていました。ところが、これは大失敗でした。高速単純計算は「考えない頭」を育て「学習を妨げる優越感」を招きました。残っ たのは直ぐに壊れてしまうガラスの自信と無意味な達成感を喜ぶ子供の姿だけでした。子供達は、表面的には計算が速く知識豊富な「できる子」なのに、実は 「考えることができない子」に育ってしまいました。考える方法を教わらなかったので計算と知識に頼らざるを得なくなっていたのです。私自身もこの時はま だ、「読み・書き・計算」が基本であり、「読み・書き・計算」を徹底すれば「考える力」は自然に育つと信じ込んでいたのです。「読み・書き・計算の力」と 「考える力」の決定的な違いに気付いていなかったのです。今私は、自信や達成感を持たせられればどんな方法でもいいわけではないことを痛感しています。幼 ければ幼いほど方法(過程)が大切なのです。なぜなら成長過程にある幼児は吸収力があるだけに方法そのものをもまるごと吸収してしまうからです。手抜きを すれば手抜きを全てマスターするのです。表面的な力を求めると見事に表面的な力だけを付けてしまうのです。見当外れの無意味な(価値のない)達成感(快 感)を味わった幼児は、無意味な行動でも達成感(快感)を得るために反復行動をとるのです。幼児期の教育は一生を左右します。従って、反射的な単純作業の 反復は必要最低限とすることが肝要なのです。ですから、幼児期の高速単純計算は厳禁なのです。ところが今でも「高速計算練習」を小学校低学年で実施してい る人がいます。これでは思考力の基本を育てるべきときに、思考力の養成とは全く反対の条件反射力(考えない力)を育てていることになります。これでは幾ら 時間があっても「考える力」を育てることはできません。そして、この条件反射教育は将来的には短絡的な考え、幼稚な判断しかできない幼児大人を作ってしま います。一度「考えない頭」に育てられた子供を軌道修正するには大変な労力を要します。子供達のためにもう一工夫しようではありませんか。 |
◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆

※子供自身が作った三角視算表

最上段が合わせて10になる数「10の補数」で、下の6段が「九九」です。
これら3つの数字の配置を思い出せるようにします。
「九九の暗唱」で答えだけを思い出すのではなく、3つの数字の配置を思い出せるように練習します。
実際に練習するときには、算数のノートに「三角計算」を書き写しながら練習するといいでしょう。
「三角計算」は書き写すという準備段階で、すでに何回も自然に「10の補数と九九」の復習をしていますので、
写すだけでも力になります。ですから、少しずつ学習に取り入れていってください。
次のような日程はどうでしょうか。
◎使用例
1日目:3つの数字のうち、1つを抜いて書き写す。※このときにも同時に復習をしています。
2日目:昨日抜いていた数字を書き込む。
3日目:指隠しで1つの数字を確認
4日目:指隠しで1つの数字を確認
5日目:指隠しで1つの数字を確認
6日目:見るだけでイメージの確認
7日目:お休み
さて、ここでもう一度確認しておきましょう。「九九」は全段言えなくてはいけないのでしょうか?
答えはNOです。言えなくていいのです。「三角計算」で覚えたものだけでいいのです。三六個でいいんです。
何の支障もないのです。
「九九」を全段暗唱しなければいけないというのは思い込みなのです。
「九九」は必ず小さい数から唱えるという約束さえ守れば、三六個でいいのです。
「9×3は?」と言われても、頭の中で3×9=27とすればいいのです。
どんなに複雑な計算でも、「九九」の大(大きな数)×小(小さな数)を使わなければできない計算などないのです。
つまり、「九九」を全段覚えるのはただの習慣だったのです。不要なのです。
右利きの人が、わざわざ訓練して左手も自由に使えるようにしなくてはいけないことなどないのです。
また、左利きの人が、わざわざ訓練して右手も自由に使えるようにしなくてはいけないこともないのです。
「両方同じように使える方がいいに決まっているから、両方訓練しなくてはいけない」という人は実際に生活をしたことがない人です。
もちろん、「九九の暗唱」は重要事項です。それは、音声がイメージを導くからです。
しかし、「三角計算」のイメージが浮かべば「九九」は三六個でいいんです。
なぜなら、反対の「九九」(大×小)は見えてしまうからです。
ただし、小学校ではみんなが「九九の暗唱」を全段します。だったら、「九九の暗唱」は歌だと思って覚えればいいんです。
半分は忘れてもいいけれど、歌のように覚えるということです。
このように、「九九」を全段覚えることは負担になるだけですから、その時間を使って筆算の構造を理解したほうが
百倍も力になります。間違っても暗算に走ってはいけません。
さらに、「三角計算」は加減乗除+分数+約分+イメージトレーニングのすべてを同時に練習することができるのです。
また、「三角計算」は視覚イメージを利用するため瞬間的に反応できますから、スピード養成の弊害もありません。
しかも、考える素となるイメージ化の練習にもなっているので、考える訓練にもなります。
「三角計算」は基礎計算力の養成と同時に、考える力の養成もしているのです。
今まで行われてきた基礎計算練習とは、「九九」をいかに高速で思い出せるかという練習でしかありませんでした。
これでは翼をつけずにプロペラだけをフル回転させている飛行機のようなものです。動きはしますが、決して飛ぶことはできません。
空を飛ぶには翼が必要なのです。また、翼があればプロペラをフル回転させる必要はないのです。
いつもフル回転させられているエンジンは疲労し、焼けついてしまい、ついには壊れてしまいます。
「九九が高速でできる」ということと、「三角計算をイメージできる」ということの間には雲泥の差があるのです。
2×6=12は二年生で習います。ところが12÷6=2は五年生です。
そして、2×6=12と12÷6=2の関係については何も意識できません。
ところが、2×6=12を「三角計算」で使えるようにすると、
すでに小二で12÷6=2や12÷2=6(分数や約分も)を見ていることになります。
つまり、12÷6=2を教わる五年生までのまるまる三年間も見続けていることになるのです。
この配置を覚えられない子は一人もいません。このように何の苦労もなく応用がきくところが「三角計算」のすごさなのです。
……………………………………………………………………………………………
●利用者の声●
先生の著作「絶対学力」を読ませて頂き、夏休み、三角計算の足し算引き算をさせました。
(本を見て、毎日手作りしました。)授業がまったく分からず、泣いていた娘が、夏休み後半には自分から進んでするようになり、
5+5=10だから、10-5=5になるんだねと、自分で笑顔で話せる位になりました。それまで、いろいろなドリルも試しましたが、
理解できた物はありませんでした。評論より、子供の反応が正解だと思います。
遅まきながら、もっと先生の教材を活用させていただければと、登録することにいたしました。よろしくお願いいたします。
……………………………………………………………………………………………
では普通の暗算と「三角計算」を比較してみましょう。
1:3×7を頭の中でやってみます。
すると、頭の中では「九九」の音声に反応して、
3:7:21
と数字が出てきます。
次に、7×3を頭の中でやってみます。
すると、頭の中では「九九」の音声に反応して、
7:3:21
と数字が出てきます。
次に、21÷3をやってみます。
が、これはできません。「割算九九 (音声)」などは教わっていないからです。
そこで、3×□=21を頭の中でやり、□=7を探します。
次に、21÷7をやってみます。
が、これもできません。
そこで、7×□=21を頭の中でやり、□=3を探します。
さて、今度は今やった計算を続けてやって、時間を計ります。
ほんの数秒のことだと思いますが、頭の中の様子をよく覚えておいてください。
3×7=
7×3=
21÷3=
21÷7=
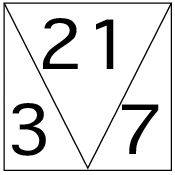
2:さて「三角計算」です。
「三角計算」では次の構図をイメージするだけです。
◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆
◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆
イメージするときのきっかけとして「九九」の暗唱を「さんしち」まで言えばスッと出てきます。
あとは見るだけで、先ほどの4つの計算に加えて分数・約分の構造も確認できます。一秒もかからないと思います。
この作業は小一でも十分にできます。絵本と同じだからです。
「九九」の暗唱はイメージするときのきっかけとしては大変優れていますので重要項目です。
ただし、苦手ならば三六個で結構です。全段スラスラと言える必要はまったくありません。
数字・文字・数式・図形・映像は、音をきっかけとして容易にイメージ化されるからです。
ここで大事なのは答えではなく、三角形に配置された3つの数字のイメージです。この形(映像)が大事なのです。
「サン・シチ・ニジュウイチ」と言ったときに 3×7=21 の21だけを意識する場合と、
「三角計算」で配置までイメージする場合とでは応用力がまったく違うということです。
3×7=21 では、前から 3:×:7:=:21 と一種類の構造を意識するだけで終わってしまいます。
ところが「三角計算」では3つの数字の配置そのものをイメージするので、
3×7=21,7×3=21,21÷3=7,21÷7=3,21/3=7,21/7=3という6種類の構造を一瞬で意識できるのです。
これは分数を教わっていない段階でもイメージできますから、分数を教わるときに新しく覚え直す必要さえないのです。
さらに、 3×7=21 は数式として見ていますが「三角計算」は絵図として見ていますから、素早く浸透し、忘れにくく
思い出しやすいという素晴らしい性質を持っているのです。
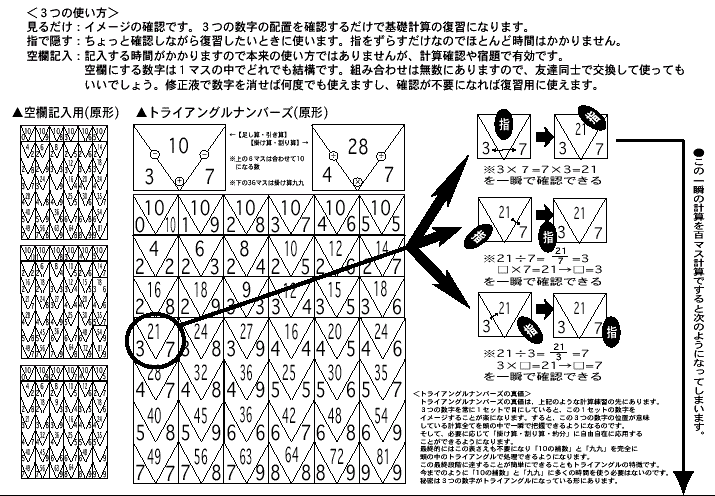
※「三角計算」使用上の注意
1:九九の暗唱は重要です。ただし、覚えたらすぐに「三角計算」に移行します。
2:「三角計算」を見ながら「九九」を言うときには、1セットに絞ってイメージ配置を覚え
ることを意識します。「九九」の暗唱は言葉に出さなくても結構です。
3:「三角計算」は暗唱の定着を目標にしているのではありません。目標は視算のためのイメ
ージ再現です。暗唱は単なるきっかけにすぎません。「三角計算」では3つの数字の「関
係」を配置によって体得できるようにしてあります。このことで計算以前の暗記である「10
の補数と九九」を、単なる暗記から応用力の基本へと引き上げることを可能にしています。
4:視算が最速だからと言って、すべての計算をイメージ操作でしようとしてはいけません。
視算は「三角計算」だけにします。たしかに、練習すればソロバンの有段者のようにイメ
ージ操作をして高度な暗算を高速でできるようになります。しかし、それは特殊技能では
あっても、不要なことなのです。すごいことですが、基礎学力ではありません。小学生の
学習には不要なのです。見栄えがいいからといって、不要なことに時間をかけている時間
はありません。この見極めが小学生の学習では重要なのです。
……………………………………………………………………………………………
※九九が苦手な人は「三角視算表」をいつも横に置いて筆算を正確に出来るようにすれば何の支障もありません。
焦って九九を暗記する必要もありませんし、ましてや役に立たない暗算の練習をする必要もありません。
大切なことは筆算の手順をマスターすることです。九九は三角視算表を見ているだけで何の苦労もなく覚えてしまいます。
……………………………………………………………………………………………
※「三角計算(視算)」以前にできること→Finger-Imageと体感計算
……………………………………………………………………………………………
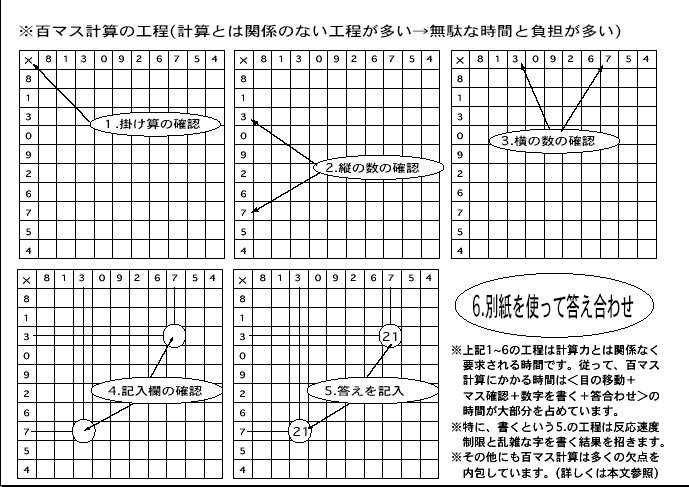
※「百ます計算」を止めた理由と改善策