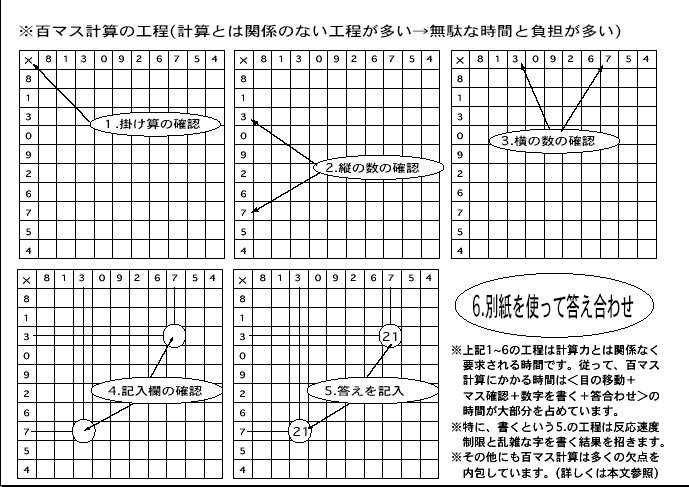
【総索引】【「ます計算」との比較】
〜トライアングルナンバーズ〜
無料提供:三角計算練習ドリル30日分(メール添付PDF書類)→ココからメールする
※閲覧・ダウンロード無料(PDF書類)
| △原形・白紙・記入用1・2・3<記入用に記入後は確認用として使用できます> △ランダム記入用・確認用<プリントアウトして直ぐに使用できます> |
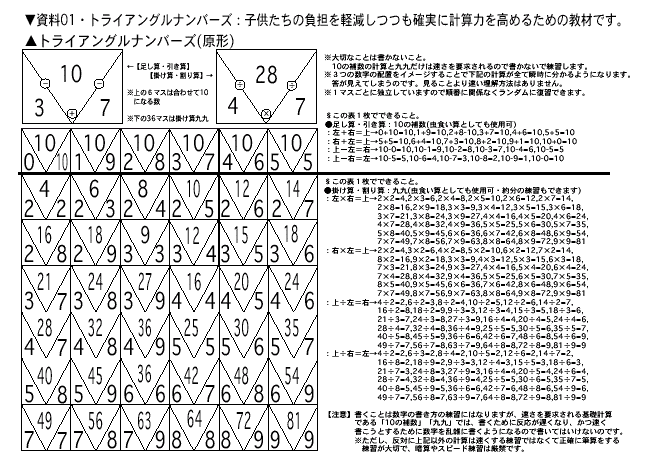
●トライアングルナンバーズはあらゆる学習に効果を発揮するイメージ操作練習機能を持っています。
ポイントは3つの数字の配置の仕方とそのイメージ化による考え方です。
この方法は「視算」と呼ばれており、人間が使える最速の基礎計算方法です。
このイメージ化はあらゆる学習を飛躍的に発展させるためには必要不可欠な基本的学力と
もなります。
※1981年に出版されたます計算を紹介している「見える学力、見えない学力(岸本裕史)」
ではます計算で九九の問題を100問完答するのに要する時間は「成績上位の子で2分以内」
「成績中位の子で3分前後」「成績下位の子で4分以上」となっています。
ところが、トライアングルナンバーズを使うと「10の補数」+「九九」を誰もが1分以内で
できるようになります。また、全体的な計算の学習時間も短くてすみますので、余裕を持っ
て考える力をつける良質の文章問題もできるようになります。トライアングルナンバーズの
もう一つの目的はこの時間の確保にあります。基礎計算にこのトライアングルナンバーズを
使うことで今まで何年もかけていた考えない計算から卒業し、考える文章問題を解く時間を
確保できるのです。
時間をかけるべきは計算ではないのです。考える力の養成なのです。このためにも
トライアングルナンバーズは必ず小学校低学年で修得すべき方法なのです。
「目で考える」学習の第一歩にもなります。
●トライアングルナンバーズは最終的には△の表さえも使わないで練習することができます。
頭の中で見る(イメージする)練習をするだけでいいからです。歩きながらでも食事をしながらでも瞬時に何も材料を使わずに練習できるのです。
※3つの数字が同時に決められた配置で「見える」ことが重要なのです。人は「見る」ことで多量の情報を瞬時に処理できるようになっているからです。あたかも、地上しか歩けなかった雛鳥が成長して大空を飛び回れるようになったかのようです。ある人は「蒸気機関車から一気にリニアモーターカーに乗り換えたようだ」とも言っていました。
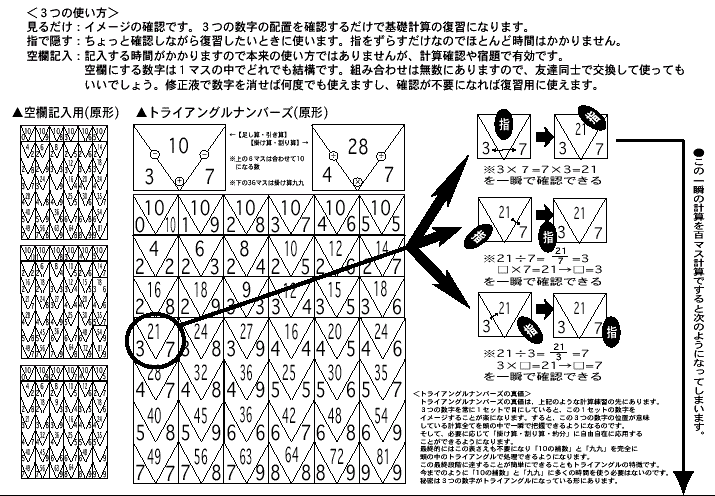
※「サンシチニジュウイチ(3×7=21)」の「サンシチニ」まで言った時には既に
頭の中にトライアングルナンバーズが見えています。すると、その頭の中の映像を
確認するだけで以下の6種類の計算
<3×7=21,7×3=21,21÷3=7,21÷7=3,21/3=7,21/7=3>
を瞬時に確認できます。
【総索引】
●リニアモーターカーがスゴイのは「速いから」ではなく、リニアモーターという今までの動力とは全く異なった次元の動力を使っているからです。
●トライアングルナンバーズがスゴイのは「速いから」ではなく、視覚思考という今までの認識方法とは全く異なった次元の認識方法を使っているからです。
※もちろん、この方法が今までなかったわけでも使われていなかったわけでもありません。ただし、今までは最も繊細な教育が必要とされる時期には使われていなかったのです。トライアングルナンバーズを使うとこの時期に視覚思考ができるのです。ここが最大のポイントなのです。
●ローマ字と漢字の認識方法が全く異なるのと同様に、今までの基礎計算の方法とトライアングルナンバーズでは認識方法が全く異なるのです。漢字は大変優れた文字です。複雑な情報を簡潔に目で提示できる機能を持っているからです。まさに、トライアングルナンバーズがやっていることです。漢字が何千年と受け継がれてきたように△の歴史はここから永遠に作られていくと思います。
・視考力という言葉が今まで無かったように、教育の現場でも「目で考える」ことを意識して教えられることはありませんでした。ところが、この視考力こそが基礎計算を驚くほど楽に高速に処理できて、なおかつ考える力を育てる基礎ともなるのです。今までの教育の失敗の大部分はこの視考力に気づかなかったことが大きな原因ではないかと思えるほどです。この視考力を使えば、小学校低学年での基礎計算、高学年での文章問題、中学校での文字式、関数、証明、図形、さらには社会人での仕事、そして人生の考え方の大きな助けとなるのです。※古来、アルキメデスの様な天才もこの視考力を存分に発揮して発明・発見をしていたのです。