【総索引】
……………………………………………………………………………………………
※三角計算練習プリント・30日分の無料閲覧・ダウンロードはコチラ→(PDF書類)
……………………………………………………………………………………………
●「脳の活性化」という言葉についての注意点→★★
●「ます計算」とトライアングルナンバーズ
●トライアングルナンバーズ(以下△)はます計算(100ます計算)を使っている中で、私自身が
感じた以下の欠点を補い、かつ考える力の養成に必要不可欠なイメージトレーニングができる
ように考案したものです。→【計算に必要な回路】付記「翼という名の守り神」
●△の真価は単なる基礎計算力アップではありません。△は視覚思考「目で考えること」による
柔軟な思考を可能にする基礎力を養うことが出来るのです。
視覚思考では多面的に物を見ることが出来ます。また、多量の情報処理が瞬時に出きることを
実感することもできます。将来的にはプレゼンテーション時の作図による説明の基礎づくり等
と計り知れない基礎力を養うことが出来ます。→英語への応用例
【「ます計算」を止めた理由+α】<要注意点>【利用者の声】【視考力を育てる】
<「ます計算」の欠点>→改善策+α
1.数字を書くことで完答に要する時間が頭打ちになる→※書く必要はない
※計算(反応)速度ではなく、数字を書く速さが限界
2.乱雑な字(数字)になる →※10の補数と九九は書く必要はない
※タイムを争うので丁寧な字を書かなくなる ※筆算を丁寧に正確に書かせる
3.計算する数字が離れていて見づらい →※数字を隣り合わせにする
4.計算する数字の交点に答えを書くので間違える →※数字を隣り合わせにする
5.答え合わせに時間がかかる →※答え合わせ不要にする
6.筆算ですべき計算まで暗算(ます)でしようとする →※暗算は限定する必要がある
7.毎回作る必要がある →※1枚で何回もできるようにする
8.数字が離れていて完全なランダム練習ができない →※ランダム練習ができるようにする
9.無駄な負担が多すぎる →※無理なく無駄なく効果的に使える
教材を作る
10.計算の基本である「10の補数」+「九九」を →※同時に練習できるようにする
同時に練習できない
11.掛け算と割り算の関係がつかめない →※掛け算と割り算の関係が分かる
ようにする
12.約分練習ができない →※約分練習もできるようにする
13.イメージトレーニングはできない →※イメージトレーニングできる構造
にする
14.九九を全部覚えていないとできない →※九九は36コでOK(半分以下)
●トライアングルナンバーズは以上のます計算(100ます計算)の欠点を全て解決している
うえに、あらゆる学習に効果を発揮するイメージ操作練習機能を持っています。
ポイントは3つの数字の配置の仕方とそのイメージ化による考え方です。
このイメージ化はあらゆる学習を飛躍的に発展させるためには必要不可欠な基本的学力と
もなります。
……………………………………………………………………………………………
※1981年に出版されたます計算を紹介している「見える学力、見えない学力(岸本裕史)」
ではます計算で九九の問題を100問完答するのに要する時間は「成績上位の子で2分以内」
「成績中位の子で3分前後」「成績下位の子で4分以上」となっています。
ところが、トライアングルナンバーズを使うと「10の補数」+「九九」を誰もが1分以内で
できるようになります。また、全体的な計算の学習時間も短くてすみますので、余裕を持っ
て考える力をつける良質の文章問題もできるようになります。トライアングルナンバーズの
もう一つの目的はこの時間の確保にあります。基礎計算にこのトライアングルナンバーズを
使うことで今まで何年もかけていた考えない計算から卒業し、考える文章問題を解く時間を
確保できるのです。
時間をかけるべきは計算ではないのです。考える力の養成なのです。このためにも
トライアングルナンバーズは必ず小学校低学年で修得すべき方法なのです。
「目で考える」学習の第一歩にもなります。
●トライアングルナンバーズは最終的には△の表さえも使わないで練習することができます。
頭の中で見る(イメージする)練習をするだけでいいからです。歩きながらでも食事をしながらでも瞬時に何も材料を使わずに
練習できるのです。私はこの方法を視算と呼んでいます。暗算の中でも最速の方法です。
※3つの数字が同時に決められた配置で「見える」ことが重要なのです。人は「見る」ことで多量の情報を瞬時に処理できるようになっているからです。あたかも、地上しか歩けなかった雛鳥が成長して大空を飛び回れるようになったかのようです。ある人は「蒸気機関車から一気にリニアモーターカーに乗り換えたようだ」とも言っていました。「ます計算」と「トライアングルナンバーズ」の間には計り知れない格差があります。
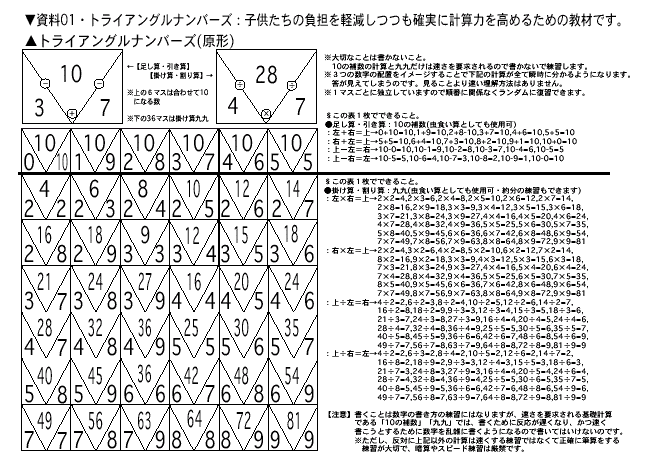
△原形・白紙・記入用1・2・3<記入用に記入後は確認用として使用できます>
△ランダム記入用・確認用<プリントアウトして直ぐに使用できます>
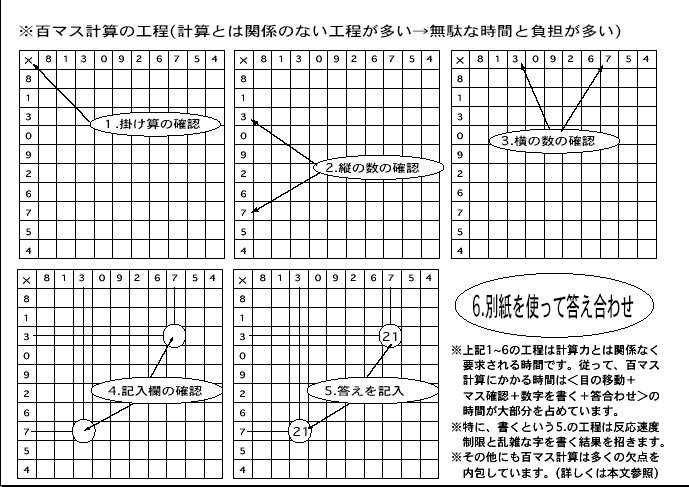
●ます計算の無駄を確認します。(無駄+速度=機械的処理→何も考えない習慣※要注意です)
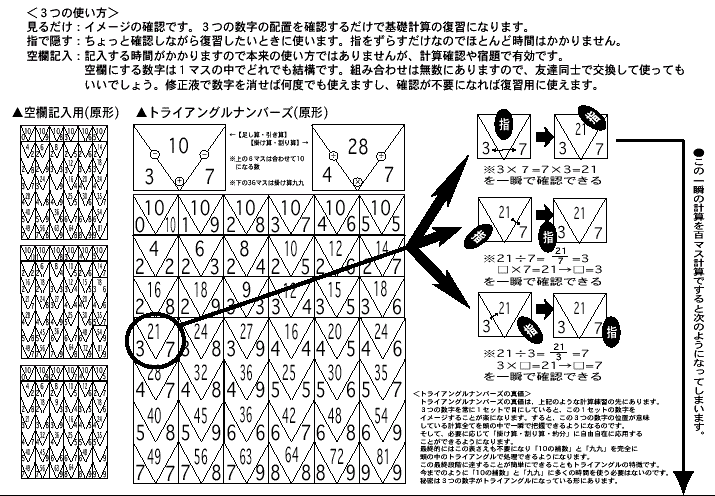
※「サンシチニジュウイチ(3×7=21)」の「サンシチニ」まで言った時には既に
頭の中にトライアングルナンバーズが見えています。すると、その頭の中の映像を
確認するだけで以下の6種類の計算
<3×7=21,7×3=21,21÷3=7,21÷7=3,21/3=7,21/7=3>
を瞬時に確認できます。
【総索引】
<要注意点>
●リニアモーターカーがスゴイのは「速いから」ではなく、リニアモーターという今までの動力とは全く異なった次元の動力を使っているからです。
●トライアングルナンバーズがスゴイのは「速いから」ではなく、視覚思考という今までの認識方法とは全く異なった次元の認識方法を使っているからです。
※もちろん、この方法が今までなかったわけでも使われていなかったわけでもありません。ただし、今までは最も繊細な教育が必要とされる時期には使われていなかったのです。トライアングルナンバーズを使うとこの時期に視覚思考ができるのです。ここが最大のポイントなのです。
●ローマ字と漢字の認識方法が全く異なるのと同様に、今までの基礎計算の方法とトライアングルナンバーズでは認識方法が全く異なるのです。漢字は大変優れた文字です。複雑な情報を簡潔に目で提示できる機能を持っているからです。まさに、トライアングルナンバーズがやっていることです。漢字が何千年と受け継がれてきたように△の歴史はここから永遠に作られていくと思います。
■視考力を育てる■〜小学校の時に「基礎計算力」と「考える力」を同時に育てる方法〜
・視考力という言葉が今まで無かったように、教育の現場でも「目で考える」ことを意識して教えられることはありませんでした。ところが、この視考力こそが基礎計算を驚くほど楽に高速に処理できて、なおかつ考える力を育てる基礎ともなるのです。今までの教育の失敗の大部分はこの視考力に気づかなかったことが大きな原因ではないかと思えるほどです。この視考力を使えば、小学校低学年での基礎計算、高学年での文章問題、中学校での文字式、関数、証明、図形、さらには社会人での仕事、そして人生の考え方の大きな助けとなるのです。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
●「10の補数と九九」は計算ではありません。あらゆる計算をするための基本ルールです。基本ルールは常に瞬時に参照できなくては役には立ちません。ただし、基本ルール以外のことは正確にできれば速い必要はないのです。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
<計算に必要な回路:「10の補数と九九」>
→「ます計算」で作られる回路には10のエネルギーを要する。これをトライアングルナンバーズ(全く違った方法)で処理すると1のエネルギーですむ。
→つまり「その回路(「ます計算」で強化される回路)はある程度必要だが」という前提さえも「その回路は必要ない」ことになります。
→さらに、トライアングルナンバーズはイメージを利用するので瞬間的に反応できる。だからスピード養成の弊害もない(最初から最速なのです)。また、考える素となるイメージ化の練習にもなっているので考える訓練にもなっている。実はトライアングルナンバーズは基礎計算力の養成と同時に考える力の養成もしているのです。今までは反対の頭の使い方だったので不可能でした。
→従って、「ます計算」は全く不要になってしまうのです。つまり、「ます計算」につかうエネルギーはどんな形であれ全て無駄に消費されていることになるのです。だから「ます計算」をすることでおこる脳の活性化はエネルギーの消費にすぎないのです。ただし「九九の暗唱」はイメージを連想させるのに必要な重要アイテムです。音声はイメージを導くことが出来るからです。
※ヒント:交通標識が「しゃりょうしんにゅうきんし」と書かれてある場合と<記号>で描かれている場合の反応を考えてみて下さい。交通標識に言葉は不要なのです。というよりも危険なので使ってはいけないのです。「ます計算」は演算記号がない分「しゃりょうしんにゅうきんし」を「車両進入禁止」と書き換えた程度の差はありますがそれだけです。本質的には変わってはいないのです。今、街中の交通標識が記号でなく漢字やひらがなになったらどうなるでしょう。間違いなく大パニックになります。至る所で交通渋滞になります。「漢字やひらがなを高速で読めるようにすればいいじゃないか(「ます計算」の理論)」という次元の話ではないのです。「ます計算」と「トライアングルナンバーズ」は「標識に於ける言葉と記号の違い」なのです。全く違う次元の話なのです。今まで教育界という街では標識を全て文字で書いていました。ですから、様々なトラブルが発生していたのです。標識を記号化するだけでこれらのトラブルは殆ど解消します。これは算数という地区だけではなくあらゆる地区に有効な方法なのです。
※文字を読めない人や読むのが遅い人でも記号ならば何の不自由もなく瞬時に反応できるので運転に支障はきたしません。これも視考力の力です。学習でも同じです。学習に使うことができる時間もエネルギーを限られているのですから、頭のエネルギーを無駄遣いするのでなく、いかに効率的に使うかが学習のキーポイントなのです。
※It's a big present for children, isn't it ?
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
「夢追い族の守り神(翼という名の視考力)」
日本のど真ん中に「限りなき夢追い族」と呼ばれる部族がK山に、「果てしなき夢追い族」と呼ばれる部族がM山にいました。両部族とも守り神は同じ神だったので、それぞれの山の頂上には翼の形をした同じ守り神を祭っていました。長年の間、両部族とも空を飛ぶことを夢みていました。空を自由に飛び回ることに憧れていたのです。両部族とも真剣に日夜努力していました。
しかし「限りなき夢追い族」の長は「速く走れるようになれば飛べる」と信じていました。また「果てしなき夢追い族」の長は「高くジャンプすれば飛べるようになる」と信じていました。時には両部族間で言い争いも起こりました。
「もう少し速く走れれば空を飛べるんだ。もう少しで飛べるんだ」
「もう少し高くジャンプできれば空を飛べるんだ。もう少しで飛べるんだ」
お互いに譲りません。この争いが起こってから時は既に数十年が経っていました。
そこへ、通りすがりの男が空からフワフワと降りてきました。両部族は言い争いをしていて、その男には全く気付きませんでした。その男は言いました。
「君達は空を飛びたいのかい」
「当たり前だ。それが夢なんだ」
と両部族が口を揃えて言いました。
すると、その男は不思議そうな顔で
「じゃあ、なぜあの翼を使わないんだい」
と山頂に飾ってある守り神を見上げました。
両部族とも一斉に笑い出しました。
「あれは守り神Shikouryoku様だ。何にも知らないんだな。よそ者は帰ってくれ」
「あれは飾りなんだ。実用品じゃないんだ。何にも知らないよそ者は帰ってくれ」
そう言って、両部族はまた走ったりジャンプしたりする練習を始めました。
この光景をジッと見ていた子供が男に近づいてきて真剣な目で言いました。
「僕、空を飛びたいんだ」
帰りかけていた男はその子に、守り神を指さして言いました。
「あれは翼と言うんだ。あれを使えば、ほんの少しの助走とほんの少しのジャンプで空を飛べるんだよ」
男は、そう言ってスゥーッと空へ帰って行きました。
子ども達は、その男が翼を使って軽々と空に舞い上がるのをしっかりと見ていました。そして、みんな大急ぎで家に帰りました。どの家にも翼は祭られていたからです。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー